TL;DR
This Summer Cohort’s QRI Visiting Scholars were tasked with memorizing thirty graphlets and recording their experience over the course of a week. We note that to do so, there usually was a preprocessing step to make the graphlets more easily memorizable, leveraging different types of memory. In particular, the following mnemonic techniques were the most effective:
- Narratives. Making stories that involved the graphlets was surprisingly effective.
- Embedding in 3D Space. Embedding particular graphlets in 3D space also aided memorization, possibly by decluttering 2D space.
- Clustering. Memorization was very rarely done in isolation – relating some graphlets to others and making groups really helped when memorizing a significant portion of the graphlets.
It was also found that other properties intrinsic to the graphlets, such as their symmetries and their planarity, made memorization easier.
Introduction
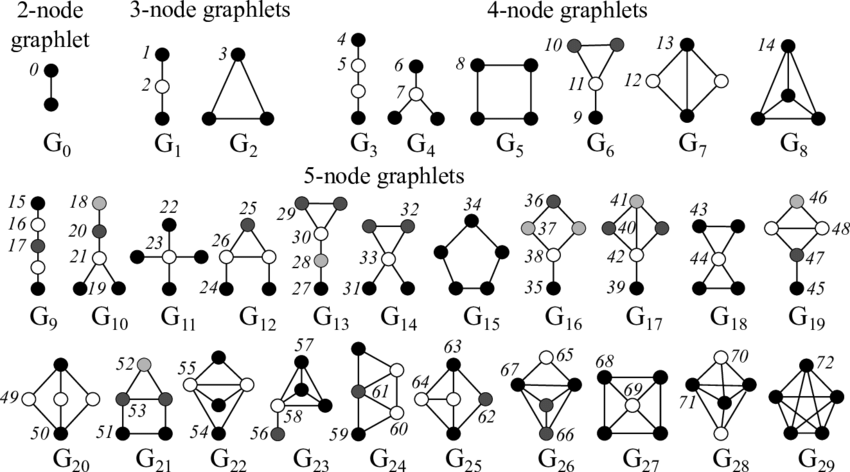
A graphlet, as the name suggests, is a small connected graph. They can certainly be useful for graph-theoretic work, but there are other reasons we may care for them. There are a total of 30 distinct graphlets (with the number of vertices between 2 and 5) up to isomorphism. These objects are simple enough that one can ask a person to memorize all 30 of them in a few days, but complex enough that their memorization will not be a trivial task, and many things can be learned from such an activity. As a refresher on these topics, we suggest Jure Leskovec’s CS224W course, and in particular this lecture which covers graphlets.
Thus, as a phenomenology exercise to kickstart the 2023 QRI Summer Cohort, the three QRI Visiting Scholars (Riccardo, Ethan and Carlos) were tasked with the memorization of the first thirty graphlets (as shown in the picture above) over the course of the first week. They had to record their experiences, as well as any phenomenological observations. In this article we present a few important observations and insights we gather from these experiences.
The Search for Easily Memorizable Representations
The set of thirty graphlets, when seen for the first time (and before any patterns are found), seem somewhat arbitrary. It is therefore noteworthy that the three Visiting Scholars, who successfully memorized the graphlets (they were tested and everyone got all the answers correct), required that the objects to be memorized were first ‘processed’ into representations that could be easily memorized by them – the graphlets are divorced enough from our experience as to make it extremely difficult to just memorize them as they are. This ‘preprocessing’ was present in all three attempts, but interestingly, it was not always deliberate, as we will see. Furthermore, different people undertook the preprocessing in different ways:
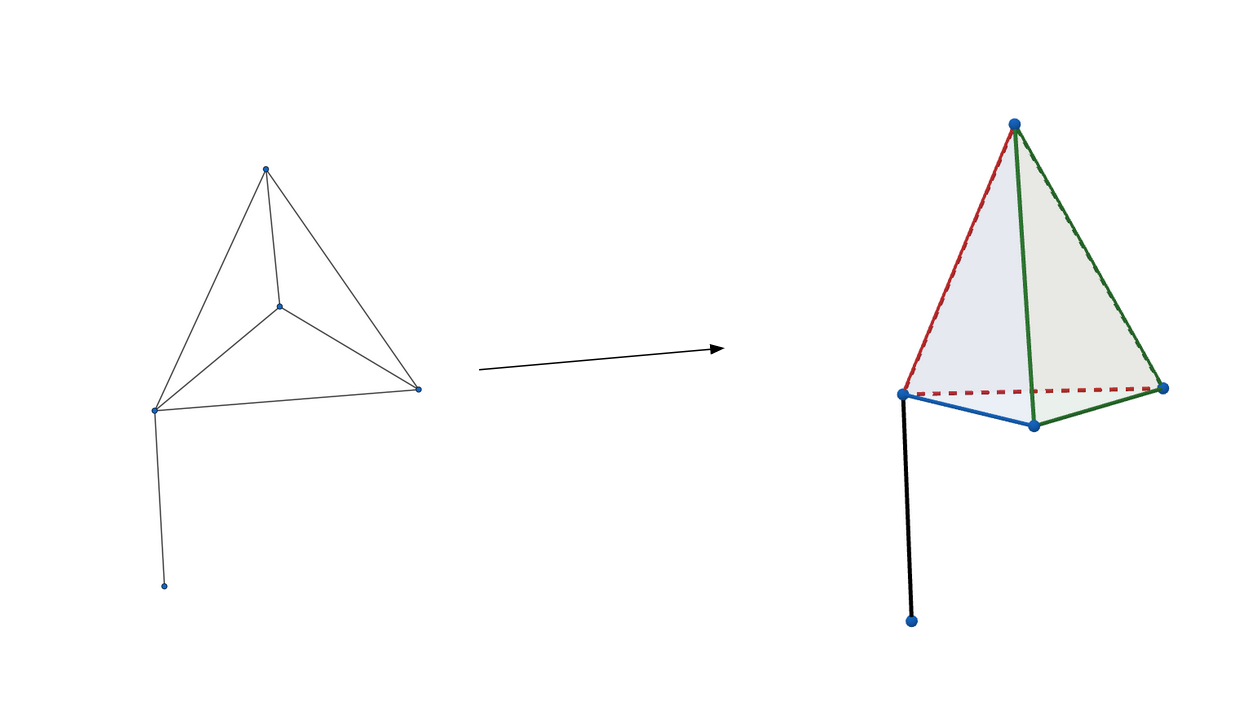
- One of the approaches that Ethan took to preprocessing was embedding some graphlets in 2D or 3D space (for instance, he found the embedding of G23 and G8 in 3D space particularly natural), thus leveraging spatial memory.
- Riccardo first tried to find explicit and/or mathematical rules that could significantly compress the information of the sequence of graphlets (thus, trying to find an easier-to-memorize representation), and which could then be decompressed to regenerate the sequence of graphlets. This approach wasn’t as fruitful as expected, and a friend suggested creating ‘stories’ with the graphlets. This approach made graphlet memorization much faster for him, as it made use of two types of memory that humans are very good at: our ability to recall stories (or narrative memory), and previous knowledge about the world (or semantic memory).
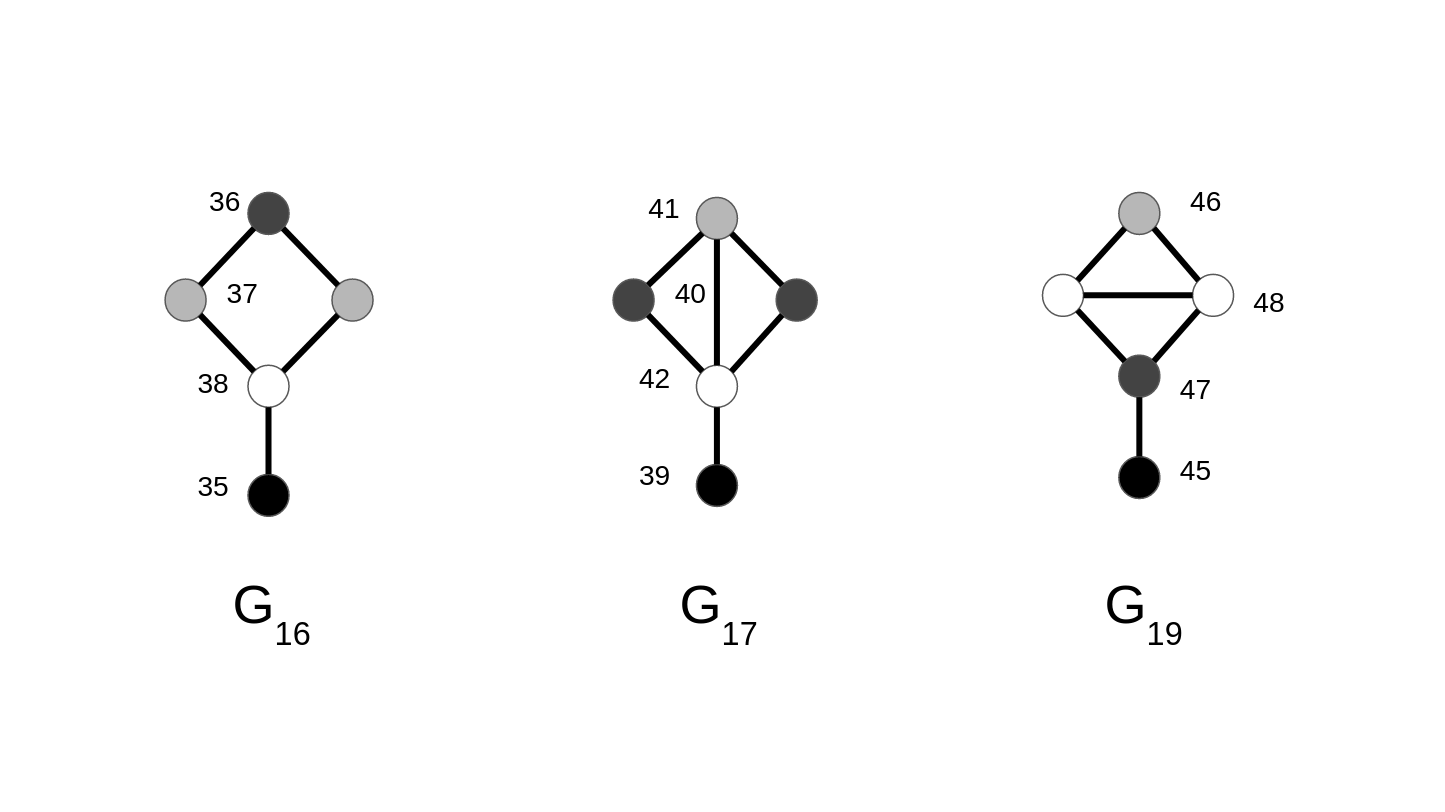
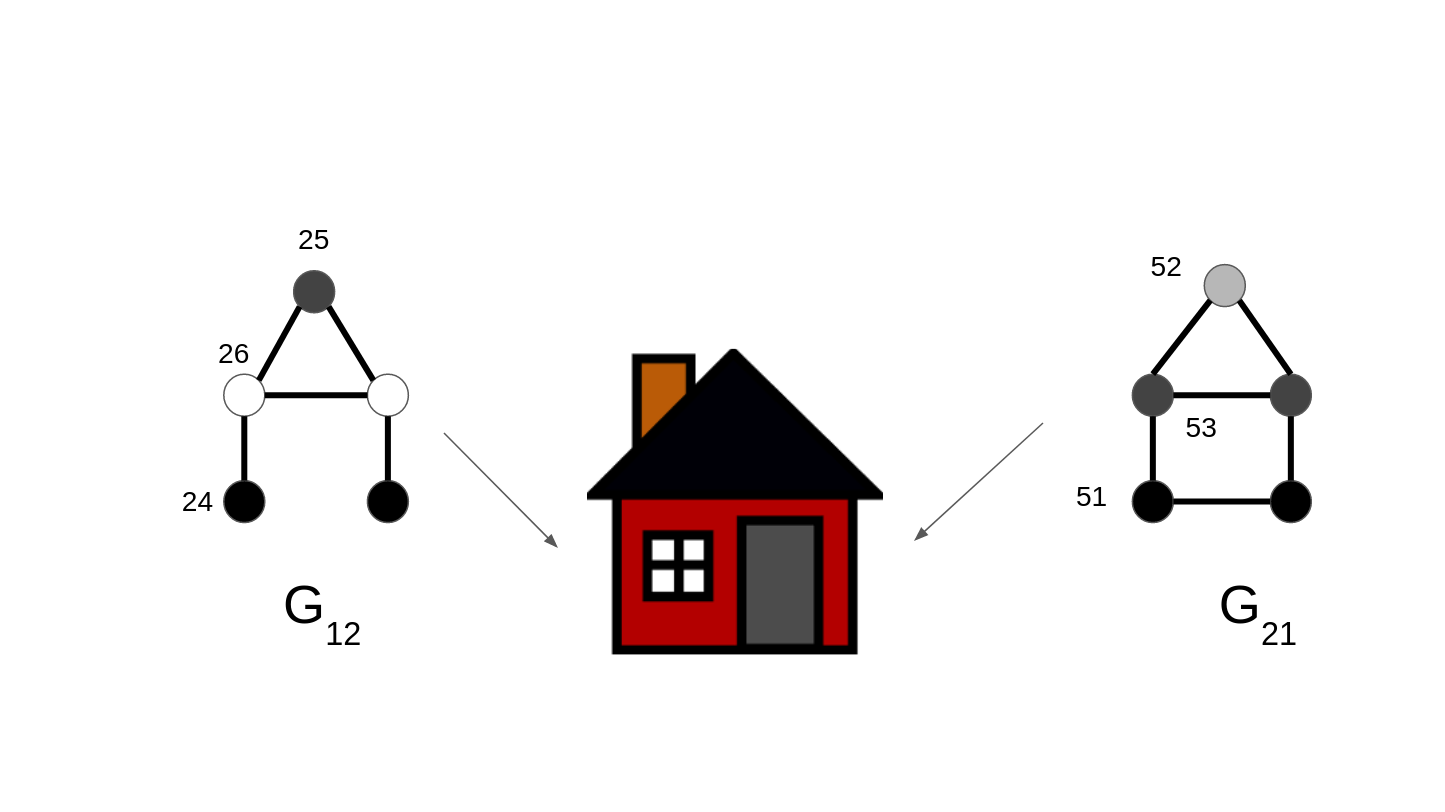
- Even when easy-to-memorize representations are not deliberately sought, these seem to emerge anyway. Carlos tried memorizing the graphlets in batches of five without deliberately adding semantic baggage – however, easy-to-memorize representations still managed to emerge (e.g. the lollipop-like patterns of G16, G17 and G19; the bridge-like structure of G24; the house-like structure of G12 and G21). Notably, similar emergent representations were reported by Ethan.
Relational and Sequential Memorization
Something common to all three memorization attempts is that they always involved taking into account, in some way or another, the relations between graphlets: the number of graphlets which were learned ‘in isolation’, without relating them to others, was low. Carlos reported first trying to learn the graphlets through spaced repetition with Anki decks, but he found it to be difficult and time-consuming (although it must be noted that it is still possible to do so) – such an approach would possibly qualify as ‘memorizing the graphlets in isolation’.
- Ethan reported that the automorphism orbits of particular sets of graphlets, such as {G16, G17, G19}, helped him with memorization – this is an example of a relation between graphlets. He also related G12 and G21 by the fact that both have house-like structures and 21 is just 12 with the digits swapped.
- Riccardo’s second approach, which involved making stories about sets of graphlets, was also fundamentally relational in nature – leveraging the fact that humans are good at remembering stories (the stories that Riccardo used to memorize the graphlets can be found in the Appendix)
- Carlos reported that when recalling a particular graphlet, he frequently had to go back to a previous graphlet that had an easy-to-memorize representation, and reconstruct all the graphlets leading up to the particular graphlet. This makes it clear that his memorization of graphlets was also strongly relational. Notably, these relations do not only emerge forwards but also backwards: to recall the last few graphlets, it was common for him to recall a graphlet that would appear later and then go backwards to the graphlet he wanted to recall.
Properties That Aid Memorization
There are representations that make use of the fact that we’re good at particular types of memory – such as narrative, or spatial. However, there are other properties that the graphlets as presented have which might also aid with memorization. Some possible properties are the following:
- The graphlets are ordered first by the number of nodes, and given two graphlets with the same nodes, the one with the least number of edges will be placed first – thus, the graphlets are loosely ordered by complexity, which, given a graphlet, gives us a hint of the sort of graphlet that might come next.
- The given representations of almost all the graphlets are planar – with the exceptions of G28 and G29 (and notably, G29 is the only one of the graphlets that has no planar representation, as it is the first to contain K5 as a minor). This might aid memorization since whenever a planar graphlet is visualized and it contains an intersection of edges, it is for certain that a vertex must lie in the intersection. This is not always the case in non-planar graphs, which might make their memorization slightly more difficult.
- Ethan also reported that some other groupings of graphlets were
natural:
- Grouping by number of cycles: All graphlets between G12 and G16 have exactly one cycle.
- Grouping by number of cycles and number of vertices per cycle: G17, G18, and G19 have 2 distinct cycles with 3 vertices.
- Natural edge additions: There were many instances of graphlets being a previous graphlet but with an added edge in a symmetrical place, or one that increases the symmetry of the graphlet, such as G20 and G22. Ethan suspects that this was one of the most load-bearing memorization mechanics (some groupings can be found in the Appendix). These ‘added edge’ relations between graphlets were very robust: Ethan reports that in these relations, the only place where one would want to add an edge without breaking significant symmetry is exactly the place where the edge appears in a later graphlet, therefore adding very little information. In this respect, the presence of cycles is particularly valuable.
Other Approaches to Graphlet Memorization
The representations used were predominantly conceptual – however, this doesn’t have to always be the case, as there are many other sorts of representations that so far have been left unexplored: the state-space of consciousness is very rich. Riccardo suggests a dance choreography or sequence of bodily moves as possibilities, which would leverage muscle memory. He also suggested another direction that might be fruitful: embodying the graphlets, and using them as objects of meditation.
Significance
Graphlets are a particularly simple mathematical structure: but by virtue of them being mathematical structures, the experience of memorizing them may certainly give us insights into the memorization of, for instance, the 17 two-dimensional wallpaper groups (as mentioned in the Algorithmic Reduction of Psychedelic States), or four-dimensional regular polytopes. And of course, memorization of objects such as these can allow us to properly mathematically describe exotic states of consciousness, such as those experienced during meditation or psychedelic experiences.
Furthermore, the kinds of memorization techniques that seem to work best, as well as their phenomenological qualities, can give us insight into how the mind works and the nature of internal representations:
- If, for instance, resonance-based mnemonic systems are particularly effective, this might suggest that our internal representations are constructed from resonant modes (which is relevant in the context of connectome and geometric eigenmodes).
- The effectiveness of embedding-based mnemonic systems (such as embedding graphlets in 3D space), may give us hints on the geometry of the field that is being instantiated (in the context of Neural Annealing), so for instance, proper instantiation of a four-dimensional geometry might provide a non-trivial advantage in the memorization of some graphlets that have a natural embedding in 4D space (such as G29).
In other words, the sorts of mnemonic techniques that are the most effective can tell us a great deal about how internal representations are created in the mind.
Acknowledgements
I want to thank the other two QRI Visiting Scholars, Riccardo Volpato and Ethan Kuntz, for their detailed descriptions of their experience memorizing graphlets, for their insightful feedback, and for our fascinating conversations clarifying some of the ideas found in this article. Furthermore, I want to thank Andrés Gómez Emilsson and Hunter Meyer for their invaluable feedback and comments on the structure and content of this article.
Notes
Riccardo (stories):
4 nodes
G3: There was a tree
G4: Which became a small starship
G5: But the small steering wheel didn’t work
G6: So they put it upside down and closed the bottom
G7: Then connected the top and bottom of the steering wheel
G8: And then to the other ends. It became a pyramid and took off.
5 nodes, part 1
G9: There was a tree
G10: Which became a big starship
G11: But the big steering wheel didn’t work
G12: So they took it to a warehouse (because it was big)
G13: Put it upside down and closed the bottom
G14: A man bent down to look at it
G15: Then called the pentagon
G16: Try a balloon, they said
G17: Or even better, a balloon with a vertical cut
G18: That’s more stable, said the man, looking more stable himself!
G19: Or even better, a balloon with a horizontal cut, which is parallel to the ground.
5 nodes, part 2
G20: Two guys liked the same three girls
G21: So they closed themselves in a sealed house of strange tables.
G22: Ordered a cone with two flavors of fried seafood
G23: They sat to eat it at a triangular table, one person sitting on the table giving food to three, but one was left out
G24: So they tried a counter with boys on one side and girls on the other, feeding with no intersections.
G25: The counter was too formal so they tried a rotated square table, with one person in the middle, but the person in the center could only serve one person at once.
G26: Meanwhile, the cone started dripping only on the side.
G27: So the person started rotating, serving everyone.
G28: By the centripetal force, the cone split into four flavors with dripping oil
G29: …which manifested divine forces of the Devil.
Carlos (notable emergent graphlet representations):
G2: Just K3.
G5: Just a square.
G8: Planar representation of K4.
G11: A cross.
G12: A house without a floor.
G13 (mentally coupled with G6): An esoteric symbol.
G15: Just a pentagon.
G16 (mentally coupled with G17 and G19): A lollipop.
G18 (mentally coupled with G14): An hourglass.
G21: A proper house.
G24: A bridge.
G29: Just K5.
Ethan (notable groupings and couplings)
G16, G17, and G19.
G12 and G21.
G12, G13, G14, G15, and G16.
G17, G18, and G19.
G20 and G22.
G26 and G28.
G25 and G27.
G28 and G29
Tags
graph theory, graphlets, mnemonics, phenomenology, math