This Qualia Research Institute publication is derived from our upcoming paper “Cessation states: Computer simulations, phenomenological assessments, and EMF theories” we submitted to the 2024 Computational Phenomenology of Pure Awareness Contest.
For a full list of resources checkout our Github.
Introduction
Cessations are fleeting states where consciousness seems to fully suspend—or “blink out”—before awareness returns.
At the Qualia Research Institute, we investigate cessations through analysis, investigation, and computational modeling. Our work integrates insights from meditation practices and the use of 5-MeO-DMT, a psychedelic known to induce cessation-like states.
We believe that studying cessations can provide valuable insights into valence, the subjective experience of pleasure and pain. These brief interruptions offer a unique opportunity to examine the structure of conscious experience. As consciousness approaches a cessation, its content simplifies and upon re-emergence it becomes more complex. By studying these transitions and their associated affective states, we seek to identify the core properties of consciousness that determine valence.
To further our understanding, we have developed simulations that model how consciousness approaches cessation states, what occurs immediately before and after, and how it transitions back out of cessation. These models feature simulations of wave patterns in phenomenal space, structural alignment across sensory modalities, and fractal recursive coherence. They are designed to support both scientific research and assist meditators and psychonauts in navigating and reporting on exotic states.
In this paper we will go over our background assumptions, theoretical framework and present three simulations related to cessations: Gestalt Detector, Standing Wave Pattern Across Multiple Fields and Fractal Recursive Coherence.
Background: The Conceptual Framework for These Simulations
- Algorithmic Reduction of Psychedelic States (Gomez-Emilsson 2016a)
- The Hyperbolic Geometry of DMT Experiences (Gomez-Emilsson 2016b)
- Symmetry Theory of Valence (Johnson 2016)
- Neural Annealing (Johnson 2019)
- Healing Trauma with Neural Annealing (Gomez-Emilsson 2021)
- Neural Field Annealing (Gomez-Emilsson 2023)
- The Constructive Aspect of Visual Perception (Lehar 2008)
- Wavefronts & Reification (Flipper 2023)
Symmetry Theory of Valence
We start with the premise that cessations are very simple, perhaps maximally simple, states of consciousness. Following Qualia Formalism (i.e., experiences correspond to precise mathematical objects whose features are isomorphic to their phenomenology) and the Symmetry Theory of Valence (Johnson 2016) as background inspiration, we explore the connection between information content and symmetry. The low information content in this case might be a really good proxy for the nature and complexity of the symmetries. We need, however, a way to quantify this “proximity to a perfectly symmetrical state”, which will of course depend on the specific formalization introduced (i.e. which mathematical objects and how to interpret their symmetries or lack thereof). This research direction suggests, however, that both valence and information content, even just in terms of what is reportable, will be highly correlated at the extreme of close to no information content. The Symmetry Theory of Valence provides a potential framework to make sense of both the success cases and failure modes for how experiencing cessations and near cessations impact the feelings of wellbeing, both during meditation, and potentially afterwards.
Andrés also speculated on the use of consonance, dissonance, and noise in connectome harmonics as an example way to quantify valence using STV as a guiding principle (Gomez-Emilsson 2017), and the present work pushes further in this direction. Namely, identifying mathematical features and models where we can approximate crisply “how far from perfect symmetry” the system is at so that we can find phenomenological correlates of positive peak valence states.
Hyperbolic Geometry of DMT Experiences
Another research thread we draw from is the Hyperbolic Geometry of DMT Experiences (Gomez-Emilsson 2016b), which enriches our framework by illustrating a dynamic model of visual hallucinations where the “world-sheet”—the spatiotemporal fabric of visual phenomena—possesses energy that influences its curvature and complexity. In DMT-induced states, heightened experiential energy causes the world-sheet to warp into intricate hyperbolic geometries, manifesting as rapidly changing and richly detailed patterns. This energy naturally crystallizes around “energy sinks,” which are areas where semantic content or recognized symmetries emerge within the experience. Attention functions as an energy source, intensifying specific features of the world-sheet, while pattern recognition acts as an energy sink, stabilizing these features by identifying meaningful patterns and symmetries. This dynamic interplay mirrors our simulation, where increasing coherence and alignment across different experiential domains lead to a collapse of complexity. As the waves within the topological pocket synchronize, different parts of the mental experience become indistinguishable, culminating in a cessation experience characterized by a unified standing wave pattern. Thus, the energy dynamics within the world-sheet framework provide a valuable perspective for understanding how alterations in the curvature and complexity of phenomenal space can lead to profound changes in consciousness, as observed during both DMT experiences and meditation-induced cessations.
Neural Annealing / Healing Trauma with Neural Annealing
Michael Edward Johnson’s concept of neural annealing offers a theoretical framework for understanding how high-energy brain states facilitate profound neural reorganization. In this model, practices such as deep meditation or the therapeutic use of psychedelics elevate the brain’s global energy levels, inducing a state of entropic disintegration where maladaptive neural patterns destabilize. This heightened energy state allows for the dissolution of rigid, maladaptive patterns, analogous to the melting phase in metallurgical annealing. As the brain “cools,” new, more harmonious neural configurations crystallize, leading to optimized information processing and integration. Moments of cessation—temporary suspensions of conscious experience reported in advanced meditative states—can be interpreted as critical transitions where old neural patterns have disintegrated, and new patterns are in the process of forming. These cessations represent pivotal points in consciousness where the energy dynamics facilitate a reorganization that contributes to lasting shifts in perception and cognition, ultimately enhancing individual and collective well-being.
Building upon Johnson’s framework, Andrés Gómez-Emilsson extends the concept of neural annealing to specifically address the healing of trauma through the lens of energy dynamics and harmonic resonance. Traumatic memories are conceptualized as microstructural dissonances within the brain’s internal representations, leading to impaired information propagation and psychological distress. By inducing high-energy states—whether through psychedelics, meditation, or other means—the brain undergoes a process where these dissonant neural patterns can be transformed into consonant ones. Gómez-Emilsson employs mathematical models of harmonic resonance and predictive coding to explain how increased neural energy leads to greater coherence and synchronization of neural oscillations. This results in a reduction of prediction errors and an enhancement of information integration across neural networks. During this transformative process, cessations may occur as the brain’s energy parameters reach levels that temporarily halt conventional conscious processing, reflecting significant neural reconfiguration. Upon resumption of consciousness, individuals often experience relief from the distress associated with trauma, indicative of the establishment of more harmonious neural configurations. By integrating Johnson’s neural annealing with Gómez-Emilsson’s mathematical and energetic models, we gain a unified understanding of how energy dynamics within the brain facilitate profound healing and transformation.
Abstraction and Reification in Gestalts
Steven Lehar’s Gestalt Bubble Model proposes that visual perception is constructed through field-like processes where waves propagate and interact within a neural medium. According to Lehar, the brain generates perceptual experiences by reifying sensory inputs into stable, volumetric representations through mechanisms akin to flame fronts and shock scaffolds. In this framework, gestalts emerge as coherent patterns formed by the synchronization of wavefronts propagating through the neural field. These gestalts exhibit consonance when the interacting wavefronts align harmoniously, resulting in stable and symmetrical percepts that require minimal energy to maintain. Conversely, dissonance arises when wavefronts interfere destructively or lack alignment, leading to unstable or conflicting percepts that are energetically inefficient.
Integrating this with the concept of neural annealing, the brain’s high-energy states facilitate the transition from dissonant to consonant gestalts by promoting synchronization across neural oscillations. During neural annealing, as described by Johnson and mathematically modeled by Gómez-Emilsson, increased neural energy allows the brain to overcome local minima in its energy landscape, enabling a global reorganization of neural patterns. This reorganization favors harmonic resonance and symmetry in line with Lehar’s field theory principles. Thus, the gestalts detected by the brain’s perceptual systems are directly influenced by the energy dynamics within the neural field: consonant gestalts represent energy-efficient, symmetrical configurations favored during neural annealing, while dissonant gestalts correspond to energetically costly, asymmetrical patterns that the brain seeks to reorganize. By aligning Lehar’s ideas on gestalt formation with the energy-centric models of neural annealing, we gain a comprehensive understanding of how harmonic resonance and energy efficiency underpin the brain’s construction of coherent perceptual experiences.
This work integrates the above background research into practice. It also incorporates more recent insights and ideas developed in preparation for the retreat, as well as insights gathered there. Specifically, personally experiencing 5-MeO-DMT at a wide range of doses and discussing its effects with a team of explorers in a legal setting for three weeks opened up new theoretical frameworks to explain what is occurring. (The retreat output, more broadly, will be published shortly).
Coupling Kernels
We noticed that during 5-MeO-DMT experiences, “everything wanted to synchronize with everything else.” While people describe other psychedelics similarly, in retrospect, the phenomenon was quite different. On mushrooms, it is not exactly the case that everything wants to synchronize with everything else. It’s more that things alternate between wanting to synchronize or anti-synchronize (i.e., be in opposite phases). And not everything is interacting with everything! At least not as obviously as with 5-MeO-DMT.
The first hint of this kind of effect came from the Tracer Tool (Gómez Emilsson 2020), where some people reported that while DMT’s tracers were very colorful, 5-MeO-DMT tended to be monochrome, favoring black or white. DMT’s tracers typically feature fast alternating complementary colors, such as neon green and magenta, which give the impression of being polar opposites on a linearized color wheel.
The thought occurred to me at the time (see the section “Modulating Lateral Inhibition” in Gomez-Emilsson 2020), that DMT might increase lateral inhibition and in turn increase the contrast between features across the predictive coding hierarchy. In contrast, 5-MeO-DMT might relax lateral inhibition, and thus reduce contrast across the entire hierarchy.
During the retreat, there was a general consensus that this explanation made a lot of sense and was congruent with people’s phenomenology.
A couple months after the retreat I started developing methods to interact with coupled oscillators in real time to figure out how to reproduce the characteristic effects we uncovered. Early this year, I came up with the idea of implementing coupled oscillators whose coupling constant across different distances can be modulated by the user - in other words, the idea was to develop a user experience that empowers an individual to modulate the geometric coupling kernel around each oscillator. And with a very broad, directional hypothesis, I did this with the aim of visualizing DMT and 5-MeO-DMT effects.
The first iteration of this concept can be found here (make sure to play some music along with it for maximum enjoyment!): Coupling Kernels 2D Grid
Here, the Coupling Kernel is applied:
5-MeO-DMT Coupling Kernels Pattern
N,N-DMT Coupling Kernels Pattern
| Neighbor Type | Coupling Constant | 5-MeO-DMT | N,N-DMT |
|---|---|---|---|
| Immediate Neighbors (Distance = 1) | K1 | 20 | -10 |
| Neighbors at Distance = 2 | K2 | 20 | 10 |
| Neighbors at Distance = 3 | K3 | 10 | -20 to +20 |
| Neighbors at Distance = 4 | K4 | 0 | 5 |
| Small-World Neighbors (Random Connections) | KSW | -20 to 20 | 0 |
Details of the Implementation
This simulation models a grid of Kuramoto oscillators, each representing a cell with a specific natural frequency and phase that evolves over time. These oscillators interact with their neighbors through coupling constants, which vary based on the (Manhattan) distance between oscillators.
Initialization and Connectivity
At the beginning of the simulation:
- Each cell is assigned a preferred frequency with spatial autocorrelation.
- Oscillators are connected to neighbors up to a Manhattan distance of 4.
- Each oscillator is also connected to two randomly chosen cells, introducing a “small-world” aspect to the network.
User Interface
The simulation includes five interactive sliders:
- Four sliders modulate local coupling constants at different Manhattan distances (1 to 4).
- One “Small World” slider modulates the coupling constant for the random long-range connections.
Mathematical Model
Phase Update Equation
For each oscillator \(i\), the phase \(\theta_i\) is updated at each time step \(\Delta t\) according to:
\[ \theta_i(t + \Delta t) = \theta_i(t) + [\omega_i + C_i] \Delta t \] Where:
- \(θ_i(t)\): Current phase of oscillator \(i\).
- \(ω_i\): Natural frequency of oscillator \(i\).
- \(C_i\): Cumulative influene on oscillator \(i\) from all of its neighbors.
Coupling Term
The cumulative influence on oscillator i from all its neighbors is given by:
\[ C_i = \frac{1}{N_i} \left( \sum_{s=1}^{4} \sum_{j \in D_s} K_s \sin(\theta_j - \theta_i) + \sum_{k \in \text{SW}_i} K_{\text{SW}} \sin(\theta_k - \theta_i) \right) \]
Where:
- \(D_s\): Set of neighbors at distance \(s\).
- \(K_s\): Coupling constant for neighbors at distance \(s\).
- \(\text{SW}_i\): Set of small-world neighbors for oscillator \(i\).
- \(N_i\): Total number of neighbors (including small-world connections).
Visualization
Each oscillator’s phase \(θ_i\) is mapped to a color using the CIELAB color space, providing a visual representation of phase patterns across the grid.
We are currently exploring the applications of the Coupling Kernels idea in a number of ways. For the purpose of this essay, we focused on how it could capture features of cessations. In particular, we combined it with the following idea (Dimensionality Interactions) to simulate Standing Waves Across Multiple Fields (see below).
Dimensionality Interactions: Metric Sharing
The QRI’s 4D Wave Simulator can help us develop an intuition for how matrix multiplication results in changes to a lattice in 4D space (using color as a signal to encode information about a fourth spatial dimension).
One of the main outcomes of the 5-MeO-DMT retreat in Canada (2023) were the countless discussions about the way the visual and somatic fields map on to each other. This was not something I in particular focused on, but Cube Flipper, Asher, and Roger Thisdell, among others all gave this a whole lot of thought and consideration. In general, it was agreed that changes in this mapping was one of the features of the experience, as if the relationship between one’s body schema and visual field was revealed to be one of the ingredients for constructing one’s world simulation all along. Because this relationship (this synesthetic mapping between sensory domains) changes only moderately at any given point in time in normal everyday life, we don’t realize the extent to which it is fabricating our sense of self and our world.
The key insight here is that there seem to be waves that can travel in the visual field and waves that can travel in the somatic field, and that their difference is part of what constructs our world simulation. Tuning into states of the system where waves are seamlessly interfacing between these two spaces will in turn be closer to cessation (and generically higher in valence, as per STV).
In the context of the necessity of an interface between two spaces of different dimensionality (e.g. 3D somatic space and 2.5D visual space) and where the system exhibits resonant modes emergent from the wiring (and coupling constant) of coupled oscillators, the system as a whole would then be predicted to minimize its energy precisely where the waves are in a low energy configuration in both the spaces that are interfacing at once. That is, one ought to achieve a projection of one space onto the other and identify a coupling kernel for each of these spaces so that the resulting space behaves as if there was only one space. When this level of coherence is achieved (good projection + good kernel) the resulting waves cannot even notice there is a projective dynamic going on. There simply is no “internal distinction” that can be found, in an otherwise really complex system that tends to find a lot of differences between the spaces it is mapping to each other.
I think that one of the things that is elegant about this framework is that it predicts that there will be likely quite specific and unique cessation conditions. Namely, combinations of spaces of different dimensions having the right projection and the right coupling kernels for them to have waves emerge that behave in the exact same way in both spaces. Perhaps some of the more exotic cessations, such as those involving a toroidal space spinning and turning inside-out correspond to some of the less intuitive “solutions” to this dynamic. Namely, where e.g. the somatic field finds a mapping to the visual field such that the waves in both do exactly the same thing and thus any sense of distinction is briefly lost.
Interacting Nested Dimensional Reduction-Amplification Spaces (INDRAS)
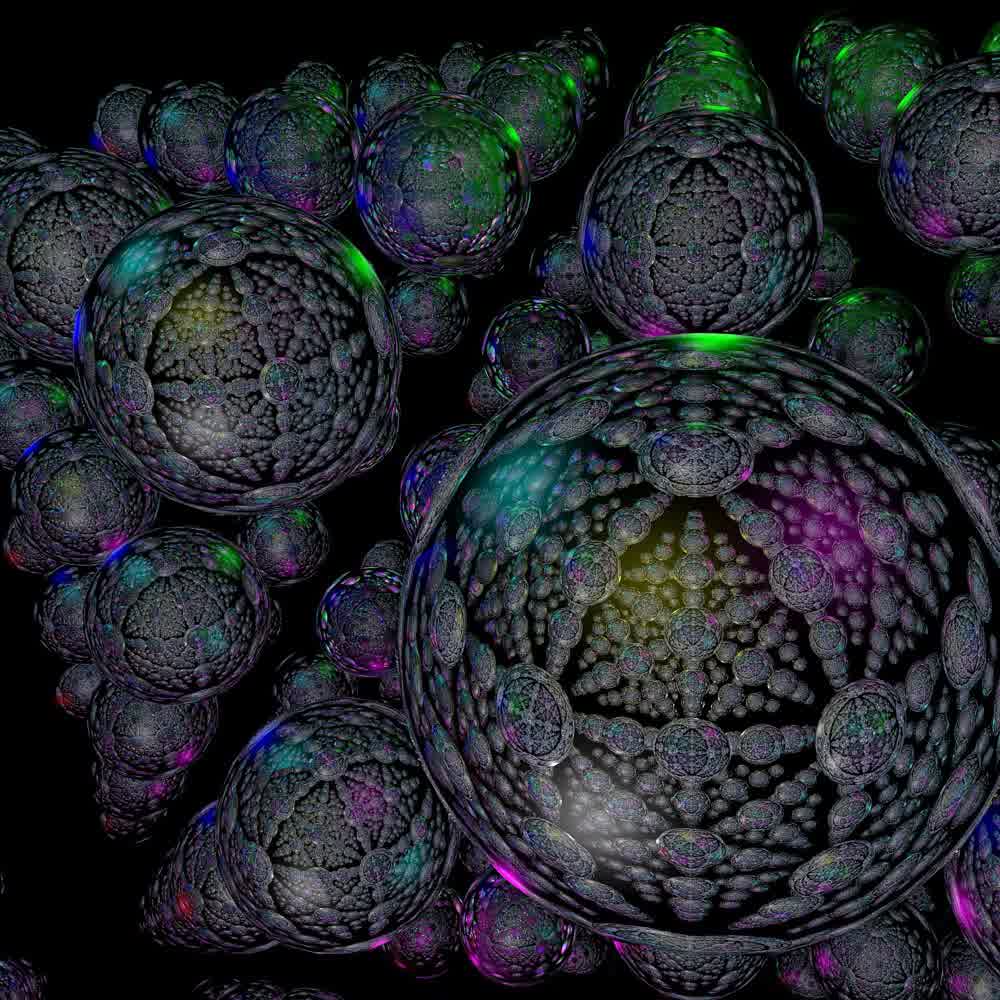
Indra’s Net is a metaphor depicting interconnectedness, where each node reflects all others, symbolizing the interdependence of all phenomena.
In order to explain Indra’s Net-type experiences I tried to reason about how different aspects of an experience shape each other (acronym is tongue-in-cheek, but we are certainly in desperate need for a good theoretical framework for Indra’s Net!). We want to have spaces of different dimensions somehow model each other recursively. And that is because many of the cessations that people have talked to me about over the years have often been described as having a very fractal quality to them. When I ask if the concept of Indra’s Net resonates as a metaphor for their experiences, they usually say yes (I don’t have a careful record, but I’d say 80% of deep meditators and psychonauts would say yes to that). The general feature of “the content seemed to reflect each other somehow” is very common. As someone who thinks that one of the computational benefits from bound experience is precisely the way in which “everything can reflect everything else”, I am drawn to these descriptions, because they sound like the sort of perceptual artifact that a very powerful computational principle might leave behind.
Say that each part of an experience requires to be contextualized by every other part for it to be in reflective equilibrium. When one opens one’s eyes on a typical human state of consciousness the scene might take about a second to stabilize and achieve this reflective equilibrium, where the meaning of each object has had a chance to propagate and inform the meaning of every other object and reached an agreement with your way of seeing (and mood, more generally). All of this means, in a way, that the stability that we need out of a system that interfaces spaces of different dimensions is quite complex. The simulation, as it were, needs to be consistent from many different points of view at once. In normal circumstances we barely notice this, since we tend to be caught up in rendering the scene from a particular point of view and as an individual. A personification of the field. But even the most bound up, contorted, tight and contracted sense of personhood still has some degree of parallax, ambiguity, superposition. No matter how much we may insist on 2D representations that crisply define each other, it is really difficult to entirely get rid of ambiguity. The way in which the meaning and quality of sensations are interdependent on each other resists any attempt to permanently “collapse and gain a sense of certainty” by any given part.
In order to simulate these kinds of dynamics I considered the following idea. If for each object that we see in the visual field, there is a kind of map from our somatic field to it. In other words, the very capacity for our visual stream to separate and group what it is there into clusters of sensations with internal connections unique to their location comes about from subtle somatic maps that track these connections. In other words, even in normal everyday life, our body is “spread out” in our visual field in multiple ways at once and we don’t even realize it. But we do this in order to track where we are in the scene, and encode hypotheticals like “what would happen if I grabbed that glass over there” in an embodied way. The texture of our world is the texture of the ways space may transform our somatic sensations. And we track this intuitively as we walk around a given space.
More so, when this mapping takes place, we have a very interesting emergent computational property. Namely, the waves in the 2D (or 2.5D as the case may be) field now allow different parts of the somatic field to talk to each other. In other words, by having multiple images in the same field, the 3D space can find shortcuts to go from one place to another. I thought that this was a very fascinating effect, in how something capable of making these projections would dynamically affect how the geodesics emerge (i.e. all of the shortest possible paths). One could posit that an experience is the “sum total of all geodesics” and in that case changing the parameters of this map changes entirely the nature of the geodesics that come about.
Indra’s Net in this case would be the result of there being different spaces, each of them possibly of different dimension or having distinct topological properties, and where each space has one or multiple maps from the other space. A cessation would perhaps be what happens when these maps look exactly the same in each and all of the spaces. Or where the geodesics all look the same.
To recap, the core idea here is that when two phenomenal spaces are coupled to each other in a way that allows multiple maps of one in the other, then we gain access to the generation of entirely new kinds of phenomenal spaces, as the shortest paths between points in either sensory modality suddenly change entirely. Each sensory field can use the other as a kind of wormhole to connect back to itself. And the more levels of recursion you allow, the more interesting the combinatorial space of possible shortest paths becomes. As a general principle, this may underlie a lot of what makes psychedelia so computationally significant: the field of experience naturally gives rise to Indra’s Net-like configurations of meta-stability as each sensory field ends with multiple maps of every other one.
These three new ideas that coalesced thanks to the lineages and the work at QRI for many years in addition to the recent retreats and post-retreat workshopping of ideas, gave rise to many different simulations that capture different aspects of the visual and tactile domains. Here we discuss in some further detail the three that we emphasized in the interviews for this study:
Gestalt Detector: Simplification via Structural Alignment
Try it yourself: Gestalt Detector: Simplification via Structural Alignment
The study of symmetries in 2D projections of 3D lattices provides insight into how transformations can simplify complex informational structures. By applying various projection angles to a 3D lattice of points onto a 2D plane, we observe the emergence of simpler, more symmetrical patterns. As the projection angles align with the lattice structure, intricate patterns simplify, with points overlapping and forming unified gestalts. This simplification process mirrors potential mechanisms of pattern recognition in perceptual systems, where complex inputs are reduced to more manageable, symmetrical forms.
To account for the flexibility of pattern recognition systems and probe the ways in which “moving towards a cessation” interacts with pattern recognition, we introduce a ‘near miss’ parameter \(\delta\). This parameter allows for the identification of “almost” equilateral triangles in the projected 2D space, where a triangle with side lengths \(a\), \(b\), and \(c\) is considered near-equilateral if \(|a - b| \leq \delta\), \(|b - c| \leq \delta\), and \(|c - a| \leq \delta\). By adjusting \(\delta\), we can explore the balance between precision and pattern recognition, mimicking the perceptual system’s ability to identify approximate symmetries. This approach provides a framework for understanding how the brain might extract meaningful structures from structured sensory inputs, mediating between the competing demands of maximizing identified patterns and minimizing perceptual dissonance—a balance that might be drastically altered when approaching a cessation event.

Perfect alignment of projection; imperfect angles
Changing symmetry/structure as angles/near miss parameters shift
Standing Wave Pattern Across Multiple Fields: Simplification via standing wave patterns
Try it yourself: Standing Wave Pattern Across Multiple Fields: Simplification via standing wave patterns
This simulation was designed to showcase scenarios where wave patterns across different systems of coupled oscillators in different geometric spaces can behave in the same way.
This is implemented through a system of coupled oscillators where the coupling strengths, and the metric to which they apply, can be dynamically adjusted by the user. We start by extending the Coupling Kernels 2D Grid to a 3D lattice. More so, we use “rings” around oscillators to parametrize the Coupling Kernels. And most important of all, we can switch between a distance function in the native 3D space of the lattice and the 2D space of the projection. In other words, we can choose to use the distances between the oscillators either in the lattice or in the screen as the distance function for the Coupling Kernel.
With this toggling between 3D and 2D representations, we simulate the interaction between sensory fields with different intrinsic dimensionalities, such as the visual field (approximated as 2.5D) and the somatic field (3D). This dimensional interplay in the tool allows us to explore how the alignment and synchronization of different sensory modalities might contribute to the emergence of unified attention, potentially leading to experiences of cessation - states of minimal informational content, maximal symmetry, and devoid of internal distinctions.
Mathematical Model
The influence function for both 3D and 2D (projected) cases is defined as:
\[ I(d) = \sum_{i=1}^n [-C_i \cdot R(d, r_i, w_i)] \]
Where:
- \(I(d)\) is the total influence at distance \(d\)
- \(n\) is the number of coupling levels (4 in this implementation)
- \(C_i\) is the \(i\)-th coupling strength (controlled by user interface sliders)
- \(r_i = D_i \cdot d_{\text{max}}\), where \(D_i\) is the \(i\)-th characteristic distance
- \(w_i = W_i \cdot d_{\text{max}}\), where \(W_i\) is the \(i\)-th ring width
- \(R(d, r_i, w_i)\) is the ring function, defined as:
\[ R(d, r, w) = \exp\left[-\frac{(d-r)^2}{2(0.5w)^2}\right] - \exp\left[-\frac{(d-r)^2}{2w^2}\right] \]
Dimensionality Interaction
The key innovation in this model is the ability to toggle between 3D and 2D representations, simulating the interaction between sensory fields with different intrinsic dimensionalities (e.g., visual field as 2.5D and somatic field as 3D). This is implemented through different distance calculations:
For 3D:
\[d = \sqrt{(\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2}\]
\[d_{max} = \sqrt{48} \text{ (assuming a 4x4x4 lattice)}\]
For 2D (projected):
\[d = \sqrt{(\Delta x)^2 + (\Delta y)^2}\]
\[d_{max} = \sqrt{\text{width}^2 + \text{height}^2}\]
The 2D case essentially “flattens” the 3D space onto a plane, ignoring the z-dimension, but still uses a continuous distance measure within that plane.
Implemenation Details
- The Coupling Kernel is implemented as a continuous function rather than discrete steps (as with “Coupling Kernels 2D Grid”).
- Euclidean distance is used instead of Manhattan distance for coupling oscillators.
- A user interface allows dynamic adjustment of coupling strengths and toggling between 2D and 3D representations.
Interpretation and Implications
Two properties of this stimulation that we hypothesize are related to cessations, and which we showed in interviews:
First, configurations of the tool (i.e. a combination of projections and Coupling Kernel values) where the waves that emerge look the same when we use the 2D or 3D distance function. In particular, the following hexagonal alignment in a state of “global coherence” (i.e. all oscillators are coupled) was a key example of a configuration where it’s impossible to tell if the waves are moving in 2D or 3D.
And second, when we use the 2D metric, we can create projection-specific and very simple standing wave patterns. For instance, we can align the dots in the lattice in the projection and then get approximately 1D resonant modes, which also move towards the general gradient of simplicity and symmetry, and thus can illustrate the process leading to a cessation.
Configurations
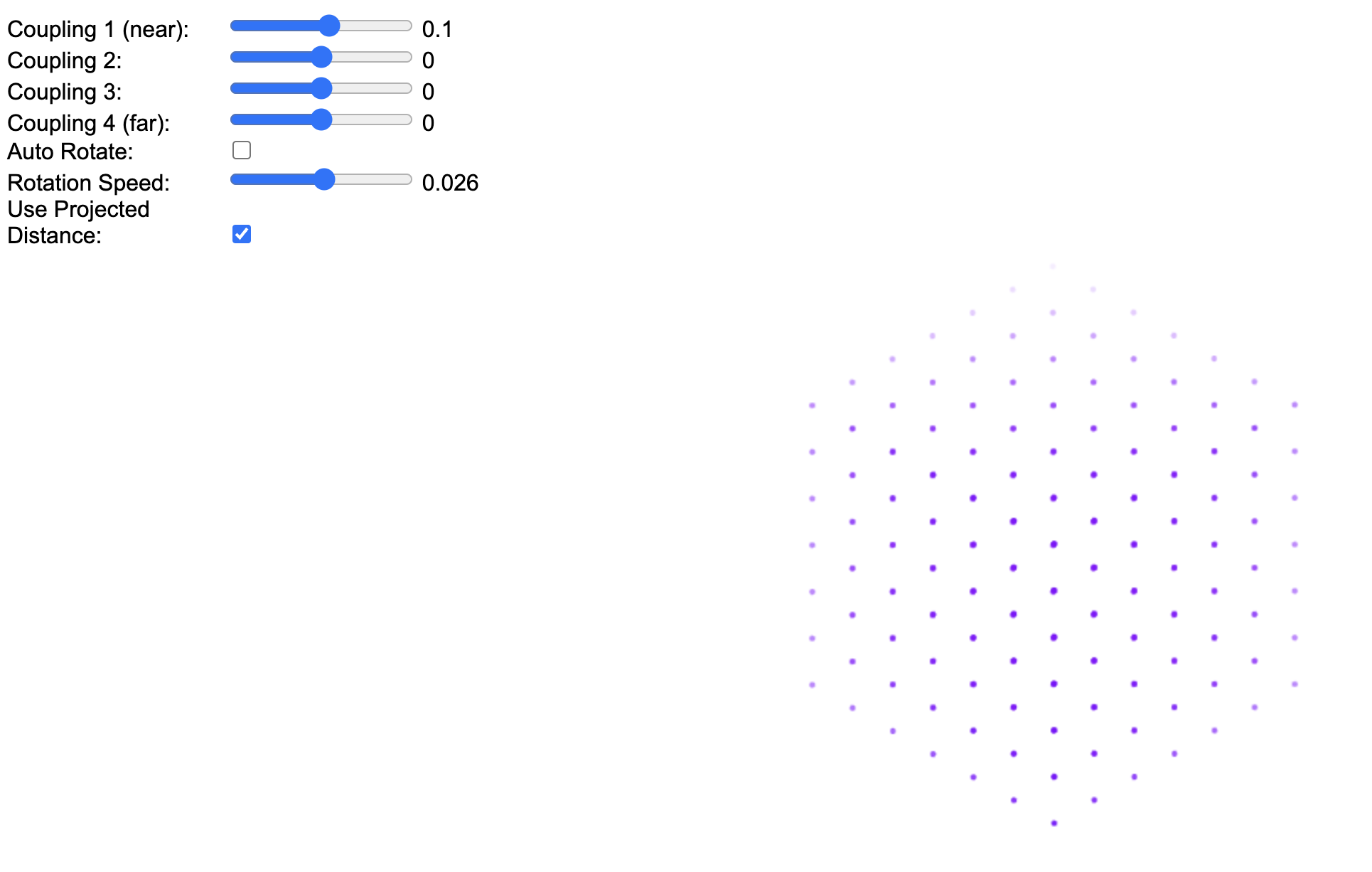
This configuration demonstrates a 2D standing wave pattern. The projection is set exactly from the corner to produce a hexagonal appearance.
This configuration is similar to the simplest configuration, but with the “Distance” parameter turned off, resulting in a 3D representation. Coupling 1 varies from -0.3 to 0.5 over 20 seconds, showing the convergence process.
| Parameter | Simplest Configuration (2D) | 3D Configuration |
|---|---|---|
| Coupling 1 | -0.1 | -0.3 to 0.5 (20s) |
| Coupling 2 | 0 | 0 |
| Coupling 3 | 0 | 0 |
| Coupling 4 | 0 | 0 |
| Auto rotate | no | no |
| Rotation Speed | N/A | N/A |
| Distance | yes | no |
| Projection | Corner (hexagonal) | Corner (hexagonal) |
This configuration showcases the transition between 2D and 3D representations with parameters exhibiting similar behavior in both dimensions. The aim is to find 2D projections where resonant modes of the simpler (projected) pattern take hold.
In this configuration, we show how using the distance in the projection we can get waves traveling in lines.
| Parameter | Transition 2D to 3D |
|---|---|
| Coupling 1 | 0.1 |
| Coupling 2 | 0 |
| Coupling 3 | 0 |
| Coupling 4 | 0 |
| Auto rotate | no |
| Rotation Speed | N/A |
| Distance | yes |
| Projection | Square lattice |
Fractal Recursive Coherence: Simplification via Recursion Collapse
Building upon the concept of the world-sheet as an energetic and dynamic system from the article on DMT geometry, the “Fractal Coherence” simulation illustrates how recursive mappings between the visual and somatic fields can lead to simplification rather than increased complexity. While this model is inspired by the energetic dynamics observed in DMT-induced states, we apply it here to 5-MeO-DMT experiences, where the overall complexity tends to decrease relative to the intensity of the state.
Fractal Recursive Coherence Simulation
The original idea of this simulation was to have multiple projections of the somatic field map onto the visual space and vice versa, creating layers of recursive interaction. Waves traveling through one field can “jump” to other parts of themselves using shortcuts provided by the alternate field. This process can generate complex, yet structured, emergent geometries as the shortest paths between points change in intricate patterns. However, under the influence of 5-MeO-DMT, these recursive interactions lead not to chaos but to convergence.
A cessation experience, in this context, would occur when these projections achieve perfect alignment, causing distinctions between them to collapse. The energy within the world-sheet crystallizes around areas of semantic content or recognized symmetries—acting as energy sinks that reduce complexity and stabilize patterns. This results in a configuration where every possible geodesic—the shortest path between any two points—is identical, and all perspectives converge into a single point of view. Without irregularities or distinctions, the emergent geometry lacks the scaffolding to construct a differentiated world simulation.
Our implementation for this proof of concept ended up being a bit simpler in a number of respects. In particular, we did not implement interaction (other than occlusions) between the projections. Instead, for tractability and simplicity, we opted for: taking a given image, “lifting it” to 3D, and then projecting it back on 2D in a number of different ways. Then, for each level of recursion, we take this output, lift it again, and project it again. The user can choose the number and type of projections as well as the angle of the lift. In essence, this still delivers the intended effect, which is that each “projection of the whole contains a model of the whole within it”. And more so, there are ways to have all of these different projections perfectly align and more or less disappear into one another.
The simulation operates as follows:
- The simulation generates a 2D grating base pattern, with precise control over its characteristics:
- Spatial Frequency X and Y directly determine the pattern’s periodicity in each direction
- Global Rotation applies an overall rotation to the entire pattern
- Grating Transparency controls the pattern’s opacity
- The Lift Dimension parameter transforms the 2D pattern into a 3D representation, adding depth and perspective to the visualization.
- The Temporal Frequency introduces time-based variation, causing the pattern to evolve dynamically.
- The interface allows for the application of multiple projective transformations
- Rotation
- Scale
- Shear
- Translation
Each projection can be individually parameterized, creating a complex composite transformation.
The simulation implements recursion on these projections, with the ability to add or remove recursion levels. Each level applies the set of defined projections to the output of the previous level, creating a number of layers or levels with cross-frequency correlations. To me, it generates the sense of a “collapse” of many points of view into just one. We thought that it captured enough features of Indra’s Net and of a fractal simplification process potentially reminiscent of cessations that it was worth including in the study.
Try it yourself: Fractal Recursive Coherence: Simplification via Recursion Collapse
Exploring the Lift Dimension Parameter
| Parameter | Value |
|---|---|
| Lift Dimension | Ranging through the entire line |
| Global Rotation | All the way to the left |
| Spatial Frequency X | All the way to the left |
| Spatial Frequency Y | Almost all the way to the left |
| Temporal Frequency | 75% |
| Grating Transparency | 25% |
| Toggle Cycle Mode | Off |
| Projection 1 | Rotation - right in the middle |
| Projection 2 | Scale - right in the middle |
| Projection 3 | Shear - right in the middle |
| Projection 4 | Shear |
| Recursion Level | 4 |
Taking Stock
The three simulations together paint a picture of how information content in experiences can hover around zero. We discuss how years of research and a recent collective work on 5-MeO-DMT phenomenology gave rise to new insights for making sense of these experiences with close to no content. We discussed how Coupling Kernels can emulate DMT vs. 5-MeO-DMT dynamics (global coherence vs. competing clusters of coherence), investigated the constraints and challenges that come with rendering our world simulation as implied by the fact that each sensory field has a characteristic dimensionality, and we considered how such communication could lead to shortcuts even within a single field. We then use these ideas to create simulations that might have phenomenological resemblance to meditative cessations and peak 5-MeO-DMT experiences. In this work, we highlight three: (1) Gestalt Detector, which shows how specific points of view interact with our capacity to detect gestalts. Conceptually, the Near Miss Depth of this simulation can be used to modulate the degree of fabrication of a scene, so to speak. (2) Standing Wave Pattern Across Multiple Fields, which allows you to compare the emergent resonant modes in a system of coupled oscillators (using Coupling Kernels) and, crucially, switch between a 3D and a 2D distance function. The hypothesis here is that cessations are states where the waves travel the same way whether we’re using the 3D or 2D distance function, symbolizing a state where different experiential fields become indistinguishable from each other. And (3) we use the concept of “recursively projecting one space into another” to model how sensations between sensory fields may form complex synesthetic constructs in exotic states of consciousness akin to Indra’s Net. For the purpose of modeling cessations, we explore how this system can collapse to a state where “all projections look the same”, and thus evoke or model a state of zero phenomenality.
Acknowledgements
I extend my deepest gratitude to Bijan Fakhri and Chris Percy for their invaluable collaboration efforts and insights during our work on cessation simulations.
Thank you to Cube Flipper, QRI’s Visual Oscillator Team, and the High Energy Awareness Research Team. Insights such as the ones presented in this paper are only the beginning of our collective work.
A special thank you to Michael Edward Johnson for years of collaboration at the Qualia Research Institute.
I am grateful to Hunter, Marcin, Maggie and other members of QRI for their unwavering support throughout this journey. Your belief in this work has been a constant source of strength.
I would like to express my sincere appreciation to the QRI donors and supporters. Without your generosity and encouragement, none of this would have been possible.
Consciousness, Computational Models, Cessation, Psychedelics, Computational Phenomenology, 5-MeO-DMT, N,N-DMT